In mathematics, the trapezoidal method, also known as the trapezoid rule or trapezium rule is a technique for approximating the definite integral in numerical analysis. The trapezoidal method is an integration rule used to calculate the area under a curve by dividing the curve into small trapezoids. The summation of all the areas of the small trapezoids will give the area under the curve.

The trapezoidal method is applied to solve the definite integral of form ^b∫_a f(x) dx, by approximating the region under the graph of the function f(x) as a trapezoid and calculating its area. Under the trapezoidal rule, we evaluate the area under a curve by dividing the total area into little trapezoids rather than rectangles.

Trapezoidal Method Formula

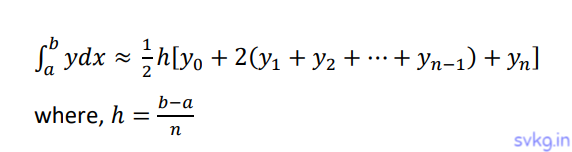
Trapezoidal Method Solved Example

C Program

//Trapezoidal Method
//This code is written by Souvik Ghosh
#include<stdio.h>
#include<math.h>

/* Define the function to be integrated here: */
double f(double x){
  return (x/(x+1));
}

/*Program begins*/
void main(){
  int n,i;
  double a,b,h,x,sum=0,integral,e=0;
  /*Ask the user for necessary input */
  printf("Enter the no. of sub-intervals(n): ");
  scanf("%d",&n);
  printf("\nEnter the initial limit(a): ");
  scanf("%lf",&a);
  printf("\nEnter the final limit(b): ");
  scanf("%lf",&b);
  /*Begin Trapezoidal Method: */
  h=fabs(b-a)/n;
  for(i=1;i<=n-1;i++){
    x=a+i*h;
    sum=sum+f(x);
  }
  integral=(h/2)*(f(a)+f(b)+2*sum);

  /*Print the answer */
  printf("\nThe answer is: %0.4f\n",integral);


}

Output Terminal