In mathematics, the Gauss elimination method is known as the row reduction algorithm for solving linear equations systems. It consists of a sequence of operations performed on the corresponding matrix of coefficients. We can also use this method to estimate either of the following:
- The rank of the given matrix
- The determinant of a square matrix
- The inverse of an invertible matrix
To perform row reduction on a matrix, we have to complete a sequence of elementary row operations to transform the matrix till we get 0s (i.e., zeros) on the lower left-hand corner of the matrix as much as possible. That means the obtained matrix should be an upper triangular matrix. There are three types of elementary row operations; they are:
- Swapping two rows and this can be expressed using the notation ↔, for example, R2 ↔ R3
- Multiplying a row by a nonzero number, for example, R1 → kR2 where k is some nonzero number
- Adding a multiple of one row to another row, for example, R2 → R2 + 3R1
The obtained matrix will be in row echelon form. The matrix is said to be in reduced row-echelon form when all of the leading coefficients equal 1, and every column containing a leading coefficient has zeros elsewhere. This final form is unique; that means it is independent of the sequence of row operations used.
C Program
//Gauss Elimination
//This code is written by Souvik Ghosh
#include<stdio.h>
void main()
{
int i,j,k,n;
float sum=0.0,c;
printf("Enter the order of matrix: ");
scanf("%d",&n);
float A[n][n+1],x[n];
printf("\nEnter the elements of augmented matrix row-wise:\n");
for(i=1; i<=n; i++)
{
for(j=1; j<=(n+1); j++)
{
scanf("%f",&A[i][j]);
}
}
for(j=1; j<=n; j++) /* loop for the generation of upper triangular matrix*/
{
for(i=1; i<=n; i++)
{
if(i>j)
{
c=A[i][j]/A[j][j];
for(k=1; k<=n+1; k++)
{
A[i][k]=A[i][k]-c*A[j][k];
}
}
}
}
printf("\nPrinting upper triangular matrix...\n");
for(int i=1;i<=n;i++){
printf("\n");
for (int j=1;j<=n;j++){
printf("%0.3f ",A[i][j]);
}
}
x[n]=A[n][n+1]/A[n][n];
/* this loop is for backward substitution*/
for(i=n-1; i>=1; i--)
{
sum=0;
for(j=i+1; j<=n; j++)
{
sum=sum+A[i][j]*x[j];
}
x[i]=(A[i][n+1]-sum)/A[i][i];
}
printf("\n\nThe solution is:\n");
for(i=1; i<=n; i++)
{
printf("x%d=%0.3f\t",i,x[i]); /* x1, x2, x3 are the required solutions*/
}
}
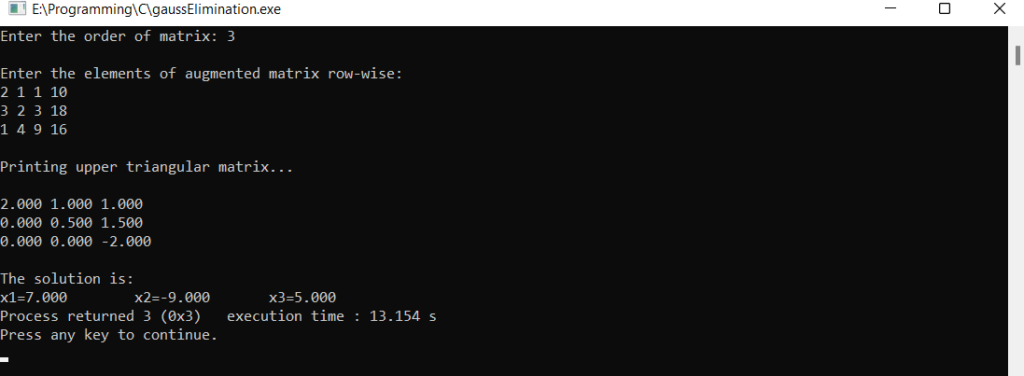
Output Terminal