Newton’s forward interpolation is a polynomial interpolation that depends on the initial value and degrees of Newton’s forward operator. The degree of polynomial fitted is one less than the number of data points. This type of interpolation is only used for equally spaced data points.
Newton’s Forward Interpolation Formula
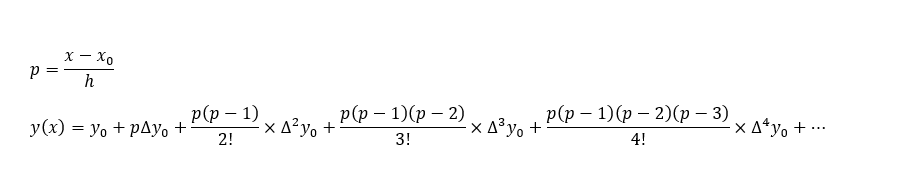
Newton’s Forward Interpolation Example
Find Solution using Newton’s Forward Difference formula
| x | f(x) |
| 1891 | 46 |
| 1901 | 66 |
| 1911 | 81 |
| 1921 | 93 |
| 1931 | 101 |
x = 1895
Solution:
The value of the table for x and y
| x | 1891 | 1901 | 1911 | 1921 | 1931 |
|---|---|---|---|---|---|
| y | 46 | 66 | 81 | 93 | 101 |
Newton’s forward difference table is
| x | y | Δy | Δ2y | Δ3y | Δ4y |
| 1891 | 46 | ||||
| 20 | |||||
| 1901 | 66 | -5 | |||
| 15 | 2 | ||||
| 1911 | 81 | -3 | -3 | ||
| 12 | -1 | ||||
| 1921 | 93 | -4 | |||
| 8 | |||||
| 1931 | 101 |

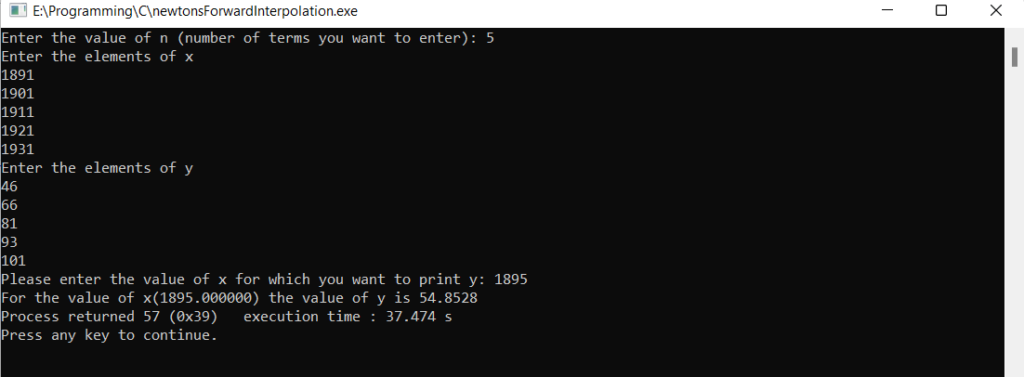
C Program
//Newton's Forward Interpolation
//This code is written by Souvik Ghosh
#include<stdio.h>
#include<conio.h>
#include<math.h>
void main(){
float h,f,p,d,s;
int i,j,n;
printf("Enter the value of n (number of terms you want to enter): ");
scanf("%d",&n);
float x[n],y[n];
printf("Enter the elements of x\n");
for(i=1;i<=n;i++){
scanf("%f",&x[i]);
}
printf("Enter the elements of y\n");
for(i=1;i<=n;i++){
scanf("%f",&y[i]);
}
h=x[2]-x[1];
printf("Please enter the value of x for which you want to print y: ");
scanf("%f",&f);
p=1;
d=y[1];
s=(f-x[1])/h;
for(int i=1;i<=n-1;i++){
for(int j=1;j<=(n-i);j++){
y[j]=y[j+1]-y[j];
}
p=p*(s-i+1)/i;
d=d+p*y[1];
}
printf("For the value of x(%f) the value of y is %0.4f",f,d);
}
Output Terminal