Newton’s backward interpolation is another way of approximating a function with an nth degree polynomial passing through (n+1) equally spaced points.
Newton’s Backward Interpolation Formula
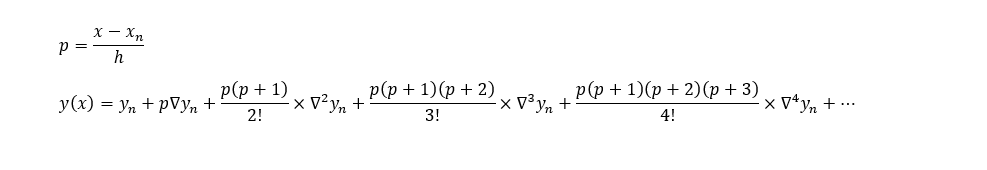
Newton’s Backward Interpolation Example
Find Solution using Newton’s Backward Difference formula
| x | f(x) |
| 1891 | 46 |
| 1901 | 66 |
| 1911 | 81 |
| 1921 | 93 |
| 1931 | 101 |
x = 1925
Solution:
The value of the table for x and y
| x | 1891 | 1901 | 1911 | 1921 | 1931 |
|---|---|---|---|---|---|
| y | 46 | 66 | 81 | 93 | 101 |
Newton’s backward difference table is
| x | y | ∇y | ∇2y | ∇3y | ∇4y |
| 1891 | 46 | ||||
| 20 | |||||
| 1901 | 66 | -5 | |||
| 15 | 2 | ||||
| 1911 | 81 | -3 | -3 | ||
| 12 | -1 | ||||
| 1921 | 93 | -4 | |||
| 8 | |||||
| 1931 | 101 |

C Program
//Newton's Backward Difference
//This code is written by Souvik Ghosh
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
float u_cal(float u, int n)
{
float temp = u;
for (int i = 1; i < n; i++)
temp = temp * (u + i);
return temp;
}
int fact(int n)
{
int f = 1;
for (int i = 2; i <= n; i++)
f *= i;
return f;
}
void main()
{
int n=0;
printf("Please Enter the number of values: ");
scanf("%d",&n);
float x[n],y[n][n];
printf("Please enter the values of x:\n");
for(int i=0;i<n;i++){
scanf("%f",&x[i]);
}
printf("Please enter the values of y:\n");
for(int i=0;i<n;i++){
scanf("%f",&y[i][0]);
}
for (int i = 1; i < n; i++) {
for (int j = n - 1; j >= i; j--)
y[j][i] = y[j][i - 1] - y[j - 1][i - 1];
}
printf("Displaying the backward difference table.....\n\n");
for (int i = 0; i < n; i++) {
printf("%0.2f\t\t",x[i]);
for (int j = 0; j <= i; j++)
printf("%0.2f\t\t",y[i][j]);
printf("\n");
}
float value = 0;
printf("Please enter the value of f\n");
scanf("%f",&value);
float sum = y[n - 1][0];
float u = (value - x[n - 1]) / (x[1] - x[0]);
for (int i = 1; i < n; i++) {
sum = sum + (u_cal(u, i) * y[n - 1][i]) /
fact(i);
}
printf("Value at %0.4f is %0.4f\n",value,sum);
}
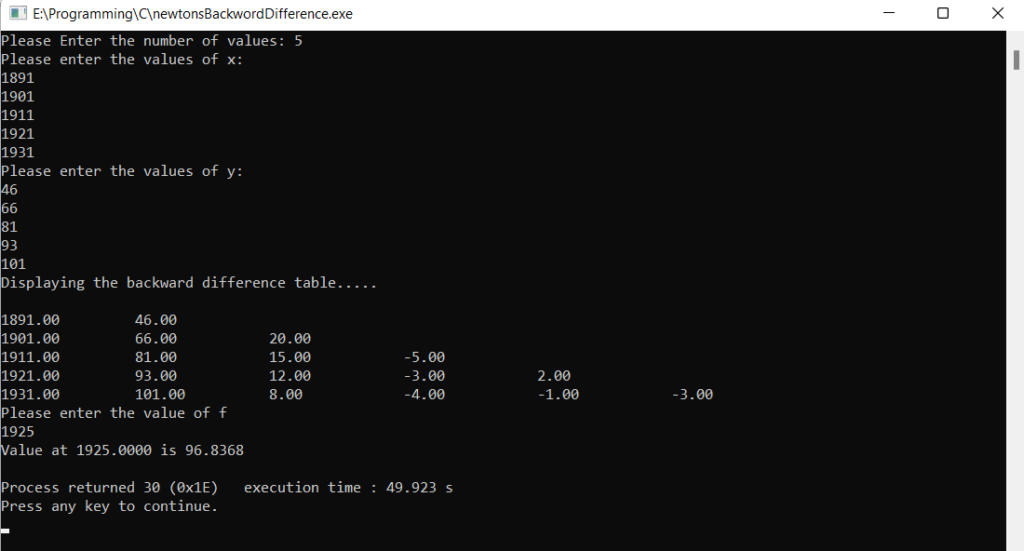
Output Terminal