Lagrange’s interpolation is also an nth degree polynomial approximation to f(x).
In numerical analysis, Lagrange polynomials are used for polynomial interpolation. For a given set of points (xj,yj) with no two xj values equal, the Lagrange polynomial is the polynomial of the lowest degree that assumes at each value xj the corresponding value yj.
Although named after Joseph-Louis Lagrange, who published it in 1795, the method was first discovered in 1779 by Edward Waring.
Lagrange’s Interpolation Method Formula
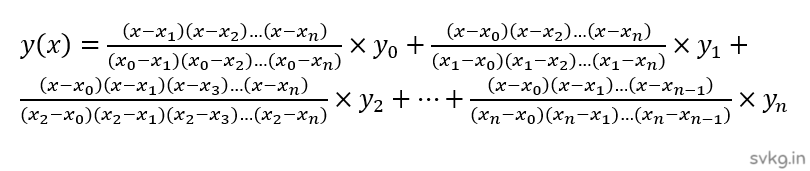
Lagrange’s Interpolation Method Example
Find Solution using Lagrange’s Interpolation formula
| x | f(x) |
| 300 | 2.4771 |
| 304 | 2.4829 |
| 305 | 2.4843 |
| 307 | 2.4871 |
x = 301
Solution:
The value of the table for x and y
| x | 300 | 304 | 305 | 307 |
|---|---|---|---|---|
| y | 2.4771 | 2.4829 | 2.4843 | 2.4871 |
Lagrange’s Interpolating Polynomial
The value of x at you want to find Pn(x):x=301
Lagrange’s formula is

C Program
//Lagrange's Interpolation Method
//This code is written by Souvik Ghosh
#include<stdio.h>
/*Function to evaluate Li(x)*/
double Li(int i, int n, double x[n+1], double X){
int j;
double prod=1;
for(j=0;j<=n;j++){
if(j!=i)
prod=prod*(X-x[j])/(x[i]-x[j]);
}
return prod;
}
/*Function to evaluate Pn(x) where Pn is the Lagrange interpolating polynomial of degree n*/
double Pn(int n, double x[n+1], double y[n+1], double X){
double sum=0;
int i;
for(i=0;i<=n;i++){
sum=sum+Li(i,n,x,X)*y[i];
}
return sum;
}
void main(){
int i,n; //n is the degree
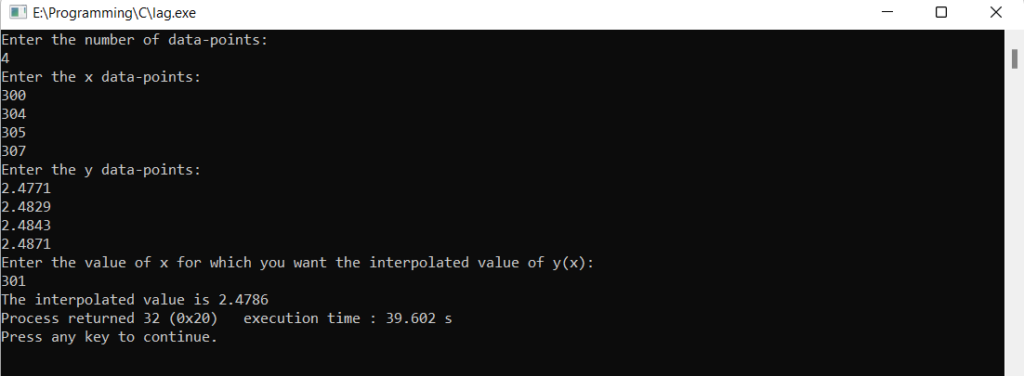
printf("Enter the number of data-points:\n");
scanf("%d",&n); //no. of data-points is n+1
n=n-1;
//Arrays to store the (n+1) x and y data-points of size n+1
double x[n+1];
double y[n+1];
printf("Enter the x data-points:\n");
for(i=0;i<n+1;i++){
scanf("%lf",&x[i]);
}
printf("Enter the y data-points:\n");
for(i=0;i<n+1;i++){
scanf("%lf",&y[i]);
}
double X; //value of x for which interpolated value is required
printf("Enter the value of x for which you want the interpolated value of y(x):\n");
scanf("%lf",&X);
printf("The interpolated value is %0.4f",Pn(n,x,y,X));
}
Output Terminal