Simpson’s 1/3rd rule is an extension of the trapezoidal rule in which the integrand is approximated by a second-order polynomial. Simpson rule can be derived from the various way using Newton’s divided difference polynomial, Lagrange polynomial and the method of coefficients. Simpson’s 1/3rd rule is defined by:
| ∫ab f(x) dx = h/3 [(y0 + yn) + 4(y1 + y3 + y5 + …. + yn-1) + 2(y2 + y4 + y6 + ….. + yn-2)] |
This rule is known as Simpson’s One-third rule.
Simpson’s 1/3rd Rule Example
Evaluate ∫01exdx, by Simpson’s ⅓rd rule.
Solution:
Let us divide the range [0, 1] into six equal parts by taking h = 1/6.
If x0 = 0 then y0 = e0 = 1.
If x1 = x0 + h = ⅙, then y1 = e1/6 = 1.1813
If x2 = x0 + 2h = 2/6 = 1/3 then, y2 = e1/3 = 1.3956
If x3 = x0 + 3h = 3/6 = ½ then y3 = e1/2= 1.6487
If x4 = x0 + 4h = 4/6 ⅔ then y4 = e2/3 = 1.9477
If x5 = x0 + 5h = ⅚ then y5 = e5/6 = 2.3009
If x6 = x0 + 6h = 6/6 = 1 then y6 = e1 = 2.7182
We know by Simpson’s ⅓ rule;
∫ab f(x) dx = h/3 [(y0 + yn) + 4(y1 + y3 + y5 + …. + yn-1) + 2(y2 + y4 + y6 + ….. + yn-2)]
Therefore,
∫01exdx = (1/18) [(1 + 2.7182) + 4(1.1813 + 1.6487 + 2.3009) + 2(1.39561 + 1.9477)]
= (1/18)[3.7182 + 20.5236 + 6.68662]
= 1.7182 (approx.)
C Program
//Simpson's one-third rule
//This code is written by Souvik Ghosh
#include<stdio.h>
#include<conio.h>
#include<math.h>
/* Define function here */
float f(float x){
return exp(x);
}
// main function
void main()
{
float lower, upper, integration=0.0, h, k,simIntegration,error;
int i, subInterval;
/* Input */
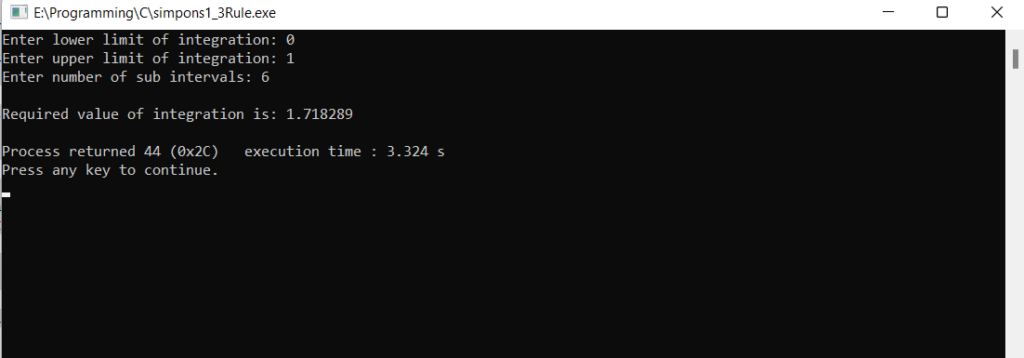
printf("Enter lower limit of integration: ");
scanf("%f", &lower);
printf("Enter upper limit of integration: ");
scanf("%f", &upper);
printf("Enter number of sub intervals: ");
scanf("%d", &subInterval);
/* Calculation */
/* Finding h */
h = (upper - lower)/subInterval;
/* Finding Integration Value */
integration = f(lower) + f(upper);
for(i=1; i<= subInterval-1; i++)
{
k = lower + i*h;
if(i%2==0)
{
integration +=2 * f(k);
}
else
{
integration +=4 * f(k);
}
}
integration = integration * h/3;
printf("\nRequired value of integration is: %.6f\n", integration);
}
Output Terminal